부동소수점 산술연산
- 부동소수점 형식은 가수 필드와 지수 필드로 이루어지므로, 부동소수점 수들 간의 산술 연산에서는 두 부분이 별도로 처리되어야 한다.
- 부동소수점 형식으로 표현된 수에서는 덧셈과 뺄셈 과정이 곱셈과 나눗셈보다 더 복잡해진다.
- 이유 : 덧셈과 뺄셈 연산에서는 먼저 두 수의 지수들이 같아지게 한 다음에 연산을 수행해야 하며, 연산이 완료된 다음에는 다시 정규화 시켜야 하기 때문이다.
- 지수들을 일치시킨다는 것은 두 수의 소수점 위치를 같게 한다는 것을 의미한다. 곱셈과 나눗셈에서는 그러한 절차가 필요하지 않다.
덧셈과 뺄셈
부동소수점 산술에서는 덧셈과 뺄셈이 곱셈과 나눗셈보다 더 복잡하다.
연산을 수행하기 전과 완료한 후에 소수점의 위치조정(alignment)이 필요하기 때문이다.
덧셈과 뺄셈 알고리즘은 다음과 같은 단계들로 이루어진다.
- 두 수의 소수점 위치를 일치시킨다(지수가 같아지도록 조정한다.)
- 가수들 간에 더하기(혹은 빼기)를 수행한다.
- 결과를 정규화 시킨다.
두 개의 10진수들 간에 덧셈을 수행하는 예 (10진 부동소수점 산술의 예시)

두 수들의 지수를 10^-3으로 일치시킨 다음에, 덧셈을 수행한다.
위의 절차는 2진 부동소수점 수에 대해서도 동일하게 적용될 수 있다.

첫 번째 단계인 지수 조정은 두 수들 중에서 더 작은 수를 우측으로 시프트(지수를 증가)시키거나, 혹은 더 큰 수를 좌측으로 시프트(지수를 감소) 시킴으로써 수행될 수 있따. 그런데 수가 저장될 정치(ex : 레지스터)의 길이가 제한되어 있기 떄문에, 시프트 방향에 따라 최상위 혹은 최하위 비트를 읽게 되는 경우가 발생할 수 있다. 그런 경우 더 작은 수를 시프트 시키면 잃게 되는 숫자가 상대적으로 작은 값이 된다.
따라서 두 수의 지수 값들이 같아질 때까지 더 작은 수를 오른쪽으로 한 비트씩 시프트 하고, 그 때 마다 지수를 1씩 증가시키는 방법을 사용하는 것이 계산 결과의 오차를 줄이는데 도움이 된다.
뺄셈도 같은 방법으로 처리할 수 있다, 가수들 간의 뺄셈을 위하여 감수를 2의 보수로 변환한 다음에 한다는 것만 다르다.
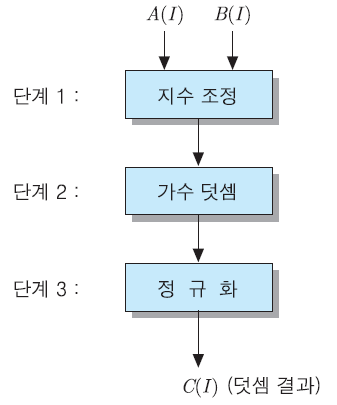
덧셈 과정은 파이프라인으로 처리하는 것도 가능하다. 즉 위의 세 단계들을 각각 파이프라인 단계로 분리하여 구현하는 것이다. 이것은 두 개의 수 배열의 요소를 연속적으로 더하는 응용에 유용하게 사용될 수 있다.
연산 과정을 독립적 단계들로 분리 가능
단계 수만큼의 속도 향상
대규모의 부동소수점 계산을 처리하는 거의 모든 슈퍼컴퓨 터들에서 채택
ex) 수 배열(number array)들 간의 덧셈
C(I) = A(I) + B(I)
곱셈과 나눗셈
부동소수점 곱셈과 나눗셈 과정은 덧셈과 뺄셈보다 더 간단하다.
곱셈과 나눗셈에서는 덧셈이나 뺄셈과는 달리 소수점 위치 조정이 필요하지 않다. 따라서 가수 사이에 직접 곱셈 혹은 나눗셈을 수행하면 되며, 지수들은 곱셈의 경우에는 더하고 나눗셈의 경우에는 뺀다. 이와 같은 계산 방법은 2진수의 경우에도 동일하게 적용된다.
2진 부동소수점 곱셈 과정
- 가수들을 곱한다.
- 지수들을 더한다.
- 결과값을 정규화한다.
첫 번째 단계는 부호를 고려하여 가수들을 곱하는 것이다. 곱셈 부분은 정수의 곱셈과 같은 방법으로 수행하면 된다. 곱셈 결과의 길이는 승수나 피승수의 두 배가 된다.
두 번째 단계는 지수들을 더하는 것이다. 만약 지수들이 바이어스된 값들이라면, 지수들을 더한 합의 바이어스 값은 두 배가 되어 있다. 따라서 그 합으로부터 바이어스 값을 한 번 빼야 한다.
마지막 단계로서, 곱셈의 결과를 정규화한다. 곱셈 과정에서 기수와 지수는 독립적으로 계산될 수 있으므로, 가산기와 승산기가 별도로 있는 경우에는 첫 번째 단계와 두 번째 단계가 동시에 수행될 수 있다.

부동소수점의 나눗셈 과정
나눗셈은 곱셈과 유사하며, 순서는 다음과 같다.
첫 단계로서 가수들을 나누고, 두 번째 단계에서는 피제수의 지수에서 제수의 지수를 뺀다. 이 과정에서 바이어스 값이 없어지므로 지수에 바이어스 값을 다시 더해야 한다. 그리고 마지막으로, 정규화 과정이 이어진다.
이러한 연산들의 과정 혹은 결과에서 발생하는 문제점들
- 지수 오버플로우(exponent overflow) : 양의 지수 값이 최대 지수값을 초과하였다. 어떤 시스템에서는 이 경우에 결과 값을 +∞또는-∞로세트한다.
- 지수 언더플로우(exponent underflow) : 음의 지수 값이 최대 지수값을 초과하였다. 이것은 그 수가 너무 작아서 표현될 수 없다는 것을 의미하는데, 이 경우에 결과 값을 0으로 세트하기도 한다.
- 가수 언더 플로우(mantissa underflow) : 가수의 소수점 위치를 조정하기 위하여 우측 시프트를 수행하는 과정에서 비트들이 가수 필드의 우측 편으로 넘치는 경우가 있다. 즉, 가수의 하위 비트들을 버리는 경우에 해당하는데, 이러한 경우에는 반올림(rounding), 혹은 절삭(truncation)이 적용될 수 있다.
- 가수 오버플로우(mantissa overflow) : 같은 부호를 가진 두 가수들을 덧셈하였을 때 올림수가 발생하는 경우가 있다. 즉, 가수의 범위가 초과된 것인데, 이 경우에는 가수를 우측 시프트 하고 지수를 증가시켜 정규화하면 된다.
➔재조정(realignment) 과정을 통하여 정규화
Reference
컴퓨터 구조론 개정 5판
https://yz-zone.tistory.com/77
[ 컴퓨터구조 ] 3.7 부동소수점 산술 연산
부동소수점 수의 산술 연산 ▣ 덧셈과 뺄셈 ▪ 지수들이 일치되도록 조정 (alignment) : (더 큰 수 기준) ▪ 가수들 간의 연산(더하기 혹은 빼기) 수행 ▪ 결과를 정규화 (normalization) [참고] 10진 부동
yz-zone.tistory.com
'CS > 컴퓨터 구조론' 카테고리의 다른 글
| 컴퓨터 구조론 5장 [기억장치- 계층적 기억장치시스템] (0) | 2025.03.29 |
|---|---|
| 컴퓨터 구조론 4장 [제어 유니트- 제어유니트의 기능과 구조] (0) | 2025.03.29 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산5] (0) | 2025.03.25 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산4] (0) | 2025.03.24 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산3] (1) | 2025.03.24 |