부동소수점 수의 표현
지수(exponent)를 이용하여 소수점의 위치를 이동시킬 수 있는 수 표현 방법
- 10진수에서는 과학적 표기(scientific notation)를 사용하여 문제를 극복할 수 있다.
- ex)274,000,000,000,000dms 2.74 * 10^14으로, 0.00000000000274는 2.74 * 10^-12으로 표기할 수 있다.
- 이 방법은 10진 소수점의 위치를 적절히 이동시키고, 소수점의 위치는 지수(exponent)를 이용하여 표시하는 것이다.
- 소수점의 위치를 필요에 따라 이동시키는 표현 방법을 부동소수점 표현이라고 한다. 그와 같이 표현된 수를 부동소수점 수라고 부른다.
- 이 표현 방법을 사용하면 매우 큰 수나 매우 작은 수도 간결하게 표현할 수 있다.
- N = (-1)^S M X B^E
- 여기서 S는 수의 부호, Md은 가수(mantissa), B는 기수(base), 그리고 E는 지수(exponent)를 각각 나타낸다. 이들 중에서 B는 10진수에서 10으로, 2진수에서는 2로 (묵시적으로) 고정되므로, 데이터 표현 형식에는 포함시키지 않아도 된다.
- 2.74 x 10^14의 경우 가수 M = 2.74, 지수 E = +14, 기수 B = 10이다.
2진 부동 소수점 수
부동소수점 표현 방식을 적용하여 표현된 2진수
- 디지털 컴퓨터에서는 2진수 체계가 사용되므로 위의 방식으로 표현하는 수는 2진 부동소수점 수(binary floating-point number)가 된다.
- 이 경우에도 구성 요소는 10진수의 경우와 동일하며, 기수 B=2인 것만 다르다. 2진 부동소수점 수는 사용되는 비트 수에 따라 32-비트 형식 혹은 64-비트 형식으로 표현된다.

- S : 1 비트, E : 8 비트, M : 23 비트
- 이러한 형식에서 가수(M)은 정밀도(precision)를 결정해주고, 지수(E)는 표현 가능한 수의 범위를 결정한다. 즉, 가수 필드의 비트 수가 많아질수록 수를 더 정확하게 표현할 수 있으며, 지수 필드의 비트 수가 많아지면 |2^E|의 최댓값이 커지므로 표현할 수 있는 수의 범위가 증가하게 된다.
- 그러나 데이터 길이가 고정된 상태에서 어느 한 필드의 비트 수를 증가시키면 다른 필드의 비트 수가 감소하므로, 적절히 조정하는 것이 필요하다.
- 데이터 형식으로 표현할 수 있는 수의 범위와 정밀도 사이의 관계를 보면 이 형식에서 지수가 2의 보수로 표현된다면, 그 범위는 -2^7 ~(2^7-1)이 된다.
- 가수 필드의 맨 좌측 비트의 왼쪽에 소수점이 있다고 가정한다면, 23-비트 가수로는 소수점 아래 23번째 자리 수(2^-23)까지 표현할 수 있다. 만약 지수 필드의 길이를 한 비트 증가시킨다면, 지수의 범위는 두 배인 -2^8 ~ (2^8 - 1)로 확장된다. 그러나 가수 필드는 한 비트가 줄어들기 때문에 소수점 아래 22번째 자리 수 (2^-22)까지만 표현할 수 있게 되어, 정밀도가 그만큼 떨어진다.
단일-정밀도 수(single-precision number)
- 32비트로 표현된 부동 소수점 수
복수-정밀도 수(double-precision number)
- 64비트로 표현된 부동소수점 수
수의 표현 범위와 정밀도를 동시에 늘릴 수 있는 방법은 데이터 표현에 더 많은 비트를 사용하는 것이다.
사용자는 위의 정밀도 수들을 필요에 따라 선택하여 사용할 수 있다.
부동 소수점 수 표현에서 어느 한 수에 대하여 여러 개의 표현이 존재할 수 있다.
이 표현들은 모두 같은 값을 나타낸다.
- 0.1101 × 2^5
- 11.01 × 2^3
- 0.001101 × 2^7
그로인한 혼란을 막는 방법은 한 가지 표준 형식을 정하여 사용하는 것이다.
정규화된 표현(normalized representation)
소수점 우측의 첫 번째 비트가 1이 되도록 지수를 조정하여 표현한 부동소수점 수
- 정규화된 표현을 사용하여 혼란을 막을 수 있다.
- ± 0.1bbb...b × 2^E
- 위의 예에서 정규화된 표현은 0.1101 × 2^5
부동 소수점 표현의 예시
부호(S) 비트 = 0
지수(E) = 00000101
가수(M) = 1101 0000 0000 0000 0000 000
소수점 아래 첫 번째 비트는 항상 1이므로, 반드시 저장할 필요는 없음(hidden bit)
→ 가수 23 비트를 이용하여 소수점 아래 24 자리 수까지 표현 가능하다.

- 부동 소수점 표현에서는 정수 0에 대한 표현이 문제가 된다. 가수는 물론 0이 되어야 한지만, 0x2^E=0이므로 지수는 어떤 수가 되어도 상관 없다. 그러나 프로그램 실행 과정에서 빈번히 이루어지는 0-검사(Zero-test)에서 데이터의 모든 비트들이 0이 아닌 경우에는 검사 과정이 복잡해진다.
- 따라서 그러한 검사가 용이해지도록 하기 위해서는 (고정소수점 수에서의 0에 대한 표현과 같이) 모든 비트들이 0이되는 것이 바람직하다. ➔크기 비교 및 0-검사가 정수 경우와 같은 방법으로 가능해진다.
바이어스된 수(biased number)
특정값(바이어스 값)을 더 하여 표현된 2진수
- 만약 E의 값이 아주 큰 음수라면 2^E의 절댓값이 거의 0에 가까워질 것이다.
- 이러한 사실에 근거하여 제안된 방법이 지수를 바이어스된 수로 표현하는 것이다. 바이어스된 수란 어떤 수에 바이어스 값이 더해진 수를 말한다.
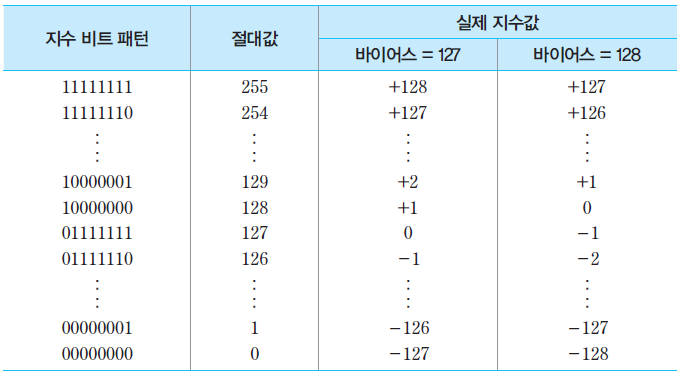
예를들어 바이어스가 3이라면 1000이 1011로 표현된다. 이것을 excess-3 코드라 한다.


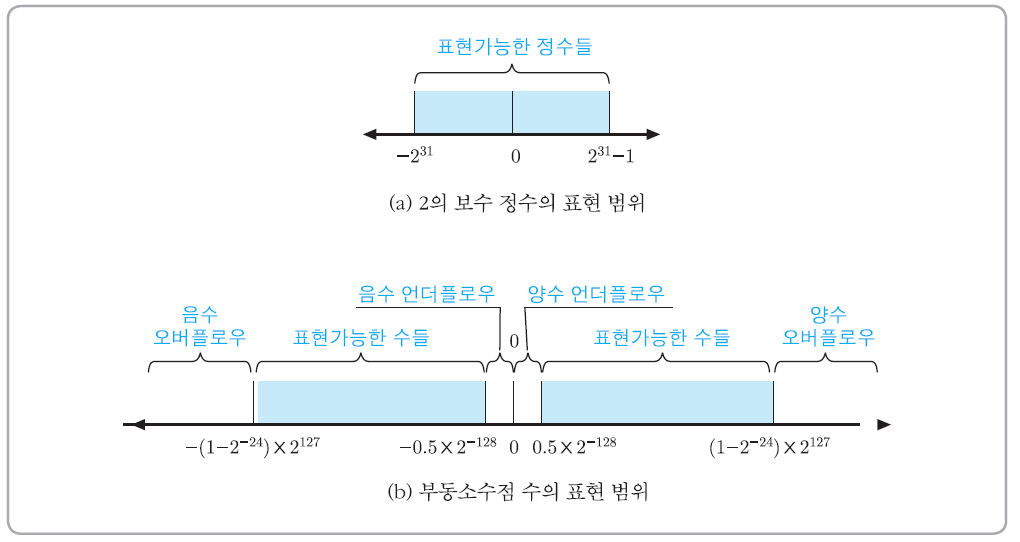
- 오버플로우는 산술 연산 결과값이 지수의 최대 양수인 127로도 나타낼 수 없을 정도로 클 경우 (ex: 2^120 x 2^-100 = 2^-220)에 발생한다.
- 언더 플로우는 그 결과값 자체가 거의 0에 근접한 매우 작은 크기이기 때문에 별로 심각한 문제는 아니다.
IEEE 754 표준 부동소수점 수의 형식
부동 소수점 수를 위한 형식과 표현 방법은 컴퓨터 회사 혹은 컴퓨터 기종마다 다르게 정의되고 사용되어 왔다. 그에 따른 컴퓨터들 간의 데이터 호환성(data compatibility)을 높이기 위해 미국전기전자공학회(IEEE)에서는 부동소수점 표현에 대한 국제 표준인 IEEE 754 부동소수점 표준 형식들을 제안하였고, 그 이후 컴퓨터 회사들에 의해 널리 채택되고 있다.
IEEE 754 부동소수점 표준 형식에서는 8-비트 길이의 지수를 가지는 32-비트 단일-정밀도 형식과 11-비트 길이의 지수를 가지는 64-비트 복수-정밀도 형식이 정의되어 있다. 이 형식들에서 기수는 2이다.

32-비트 단일-정밀도 부동소수점 수의 표현

- 가수 : 부호화-크기 표현 사용
- 지수 필드 : 바이어스 127 사용
- 1.M × 2^E의 형태를 가지며, 소수점 아래의 M 부분만 가수 필드에 저장한다. (소수점 왼쪽의 저장되지 않는 1을 hidden bit 라고 부름)
숨겨진 비트(hidden bit)
IEEE 부동 소수점 형식인 1.Mx2^E로 수를 표현할 때 정밀도를 높이기 위하여 가수 필드에는 나타내지 않는 맨 앞의 1을 말한다.
64-비트 복수-정밀도 부동 소수점 수의 표현

64비트 복수-정밀도 부동소수점 형식을 사용하는 경우에는 지수가 11비트이고 가수는 52비트이므로 , 그형식으로 표현된 2진수에 대한 10진수는 위와 같은 식을 이용하여 변환할 수 있다.


- IEEE 표준에서는 부동소수점 산술과정에서 나타날 수 있는 몇 가지 특수한 경우에 대한 정의들도 포함하고 있다.
- 만약 산술 계산 결과가 이 형식으로 나타낼 수 없는 경우에 해당한다면, NaN(Not a number)이라고 불리는 특수 코드로 표현된다.
- NaN결과를 가져올 수 있는 연산의 예로는 0으로 나누기(divide by zero), 음수에 대한 루트 계산(square root of a nagative numbeR)등과 같은 중요한 계산 오류들이 있다.
- 이 표준에서 정의하고 있는 NaN 형식은 M != 0이 아니고 E = 255(32-비트 형식) 혹은 E=2047(64-비트 형식)로 나타낸다. 즉, 가수필드의 모든 비트들은 0으로, 지수 필드는 모두 1로 세트한다. 반면에 언더플로우가 발생하면, 그 결과가 0은 아니지만 정규화 형태로는 표현할 수 없을 정도로 작은 수라고 볼 수 있다.
- 이 경우 지수 필드의 모든 비트들을 0으로 세트하고 (E=0), 가수는 비정규화된 형태(denormalized form)로서 0.M, 즉 소수점의 좌측 비트로서(1이 아닌) 0을 사용하여 수를 표현할 수 있도록 허용한다.
- 이 형식에서 0에 대한 표현은 지수 및 가수 필드의 모든 비트들을 0으로 세트하고, 부호 비트는 0(+0인 경우) 혹은 1(-0인 경우)로 세트한다. 따라서 비정규화된 형태를 이용하여 극히 작은 수를 표현하면, 그 비트 패턴은'0'에 대한 표현과 거의 같아진다.

부동 소수점 표준 형식의 필요성은 마이크로 프로세서가 출현하면서부터 대두되엇는데, 하계 전문가들과 산업체 대표들이 모여 많은 토론과 연구 끝에 1985년에 비로소 IEEE 754-1985가 공식적인 표준으로 발표되었다. 이 표준은 2008년도에 수정본이 발표될 때까지 23년간 표준으로 사용되었다. 2008년에 발표된 새로운 버전인 IEEE 754-2008에서는 몇 가지 세부적인 정의들이 추가되었는데, 특기할 사항은 4배수 정밀도(quadruple-precision : 128비트)형식이다. 4배수 정밀도 수의 형식은 지수 필드가 15비트,. 가수 필드가 112비트로 정의되었다.

이 형식에서 지수의 바이어스 값은 (2^14-1) = 16383이며, 지수의 범위는 -16382 ~ +16383이 된다. 결과적으로, 이 형식으로 표현된 2진수에 대한 10진수는 식을 이용하여 변환할 수 있다.

IEEE 754 형식들에 대한 주요 파라미터들

- 최대 지수값과 최소 지수값은 NaN과 0에 사용되는 지수 표현을 제외한 것이다.
- 단일 정밀도 형식을 이용하여 표현할 수 있는 최대 양수를 10진수로 구하면 (2-2^-23)x2^127 = 3.4 x 10^38이 되며, 최소 양수는 1.0 x 2^-126 = 1.17 x 10^-38이 된다.
- 음수에 대한 최대 및 최소 표현도 동일한 절대값을 가지며 부호만 다르다. 위의 표에는 각 형식에 대한 대략적인 최소값과 최대값도 포함되어 있다.
Reference
컴퓨터 구조론 개정 5판
https://yz-zone.tistory.com/76
[ 컴퓨터구조 ]3.6 부동소수점 수의 표현
부동소수점 수의 표현 ▣ 부동소수점 표현(floating-point representation) ▪ 소수점의 위치를 이동시킬 수 있는 수 표현 방법 ➢수 표현 범위 확대 ▣ 부동소수점 수(floating-point number)의 일반적인 형태
yz-zone.tistory.com
'CS > 컴퓨터 구조론' 카테고리의 다른 글
| 컴퓨터 구조론 4장 [제어 유니트- 제어유니트의 기능과 구조] (0) | 2025.03.29 |
|---|---|
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산6] (0) | 2025.03.25 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산4] (0) | 2025.03.24 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산3] (1) | 2025.03.24 |
| 컴퓨터 구조론 3장 [컴퓨터 산술과 논리 연산2] (0) | 2025.03.24 |