프로세서들이 기억장치 모듈을 사용하는(소유하는) 방식에 따라 크게 다음과 같이 분류
- 공유-기억장치 시스템(shared-memory system)
- 분산-기억장치 시스템(distributed-memory system)
공유-기억장치 시스템 구조
이 시스템 구조는 밀결합 형태로서, 주기억장치가 어느 한 프로세서에 속하지 않고 모든 프로세서들에 의해 공유된다.
각 프로세서는 특수 프로그램(하드웨어 초기화와 진단 프로그램)을 저장하고 잇는 적은 용량의 지역 기억장치(local memory)를 별도로 가질 수는 있으나, 운영체제와 사용자 프로그램 및 데이터들은 모두 공유 기억장치에 저장된다.
장점
- 프로세서들이 공통으로 사용하는 데이터들이 공유 기억장치에 저장되므로, 별도의 프로세서 간 통신 메커니즘이 필요하지 않다.
- 프로그램 실행시간 동안 각 프로세서들이 처리할 작업들을 동ㅈ거으로 균등하게 할당할 수 있기 때문에, 프로세서 이용률을 극대화할 수 있어서 시스템 효율이 높아진다.
단점
- 프로세서들과 기억장치들 간의 통로(버스 또는 상호 연결망) 상에 통신량이 많아지기 때문에 경합으로 인한 지연 시간이 길어질 수 있다.
- 두 개 이상의 프로세서들이 공유자원(기억장치 모듈 또는 I/O 장치)을 동시에 사용하려는 경우에는 한 개 이외의 프로세서들은 기다려야 한다.
결과적으로 이 구조를 가진 시스템에서는 프로세서 수가 증가하더라도 성능 향상이 선형적으로 이루어지지 못하게 된다. 이러한 단점을 보완하기 위해 여러가지 방법들이 사용된다.
대표적인 방법
- 고속 상호연결망과 캐시의 사용이 있다.
공유-기억장치 다중프로세서시스템에서 가장 널리 사용되고 있는 상호 연결 구조들
- 버스
- 크로스바 스위치
- 다단계 상호연결망(Multistage Interconnection Network:MIN)
버스
- 가장 간단한 연결방식으로 모든 시스템 요소들(프로세서, 기억장치 및 I/O 장치)이 하나의 시스템 버스에 접속된다.
장점
- 하드웨어가 매우 간단하다
단점
- 모든 요소들 간의 통신이 하나의 버스를 통하여 이루어지기 때문에 버스 경합이 높아져서 지연 시간이 길어진다.
- 이에 따른 성능 저하를 보완하기 위해 버스의 전송 속도를 높이거나 각 프로세서가 캐시를 가지도록 하는 방법이 사용되고 있다.
- 현재 공유-버스 구조는 프로세서의 수가 20개 정도인 중형급 컴퓨터시스템에서 주로 채택되고 있다.
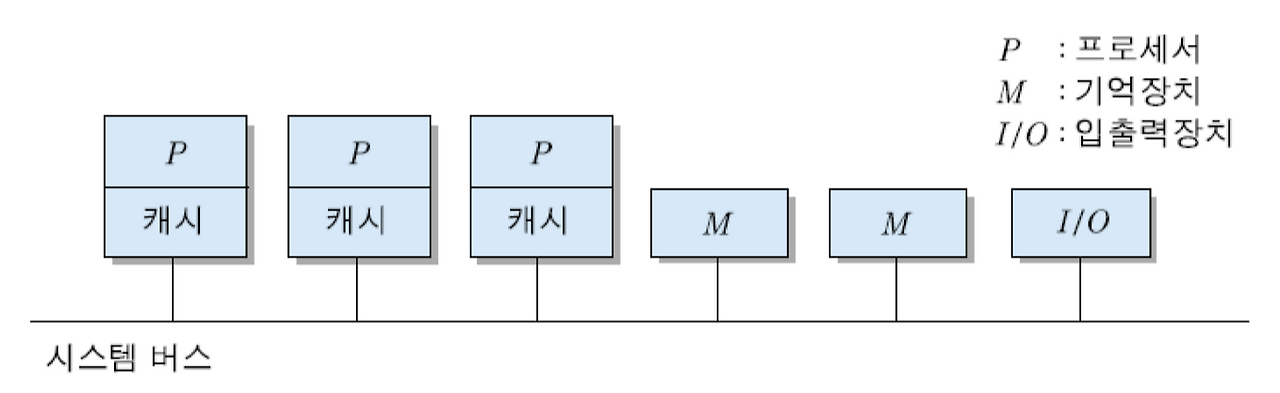
다중-버스 구조
- 버스 경합을 줄이기 위하여 두 개 이상의 버스들을 설치하는 시스템 구조
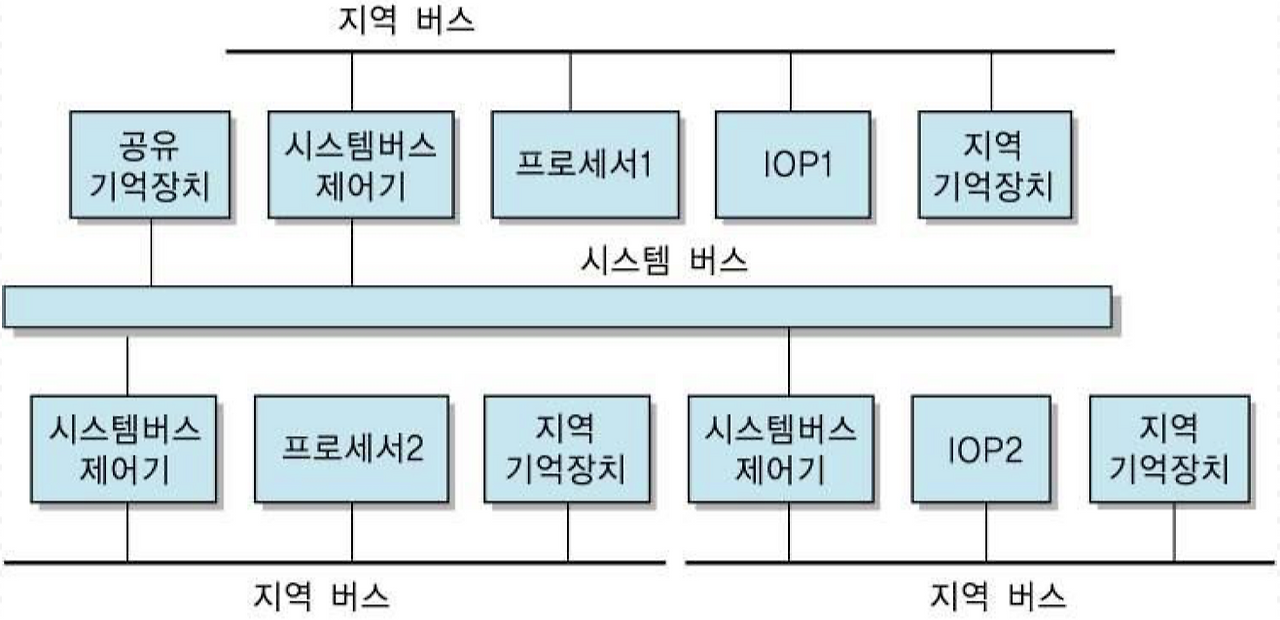
- 각 프로세서가 자신의 지역 기억장치 및 I/O 프로세서와 연결되는 지역 버스를 가직 ㅗ있고, 공유 기억장치를 사용할 때만 시스템 버스를 사용하는 계층적 버스 구조를 보여준다.
계층적-버스 구조
- 시스템 버스 외에도 용도별 지역 버스들이 설치되는 시스템 구조
- 이러한 시스템에서는 각 프로세서가 실행할 프로그램 코드와 그에 필요한 데이터는 지역 기억장치에 저장하고, 모든 프로세서들이 공통으로 사용하는 프로그램과 데이터만 공유 기억장치에 저장하게 된다.
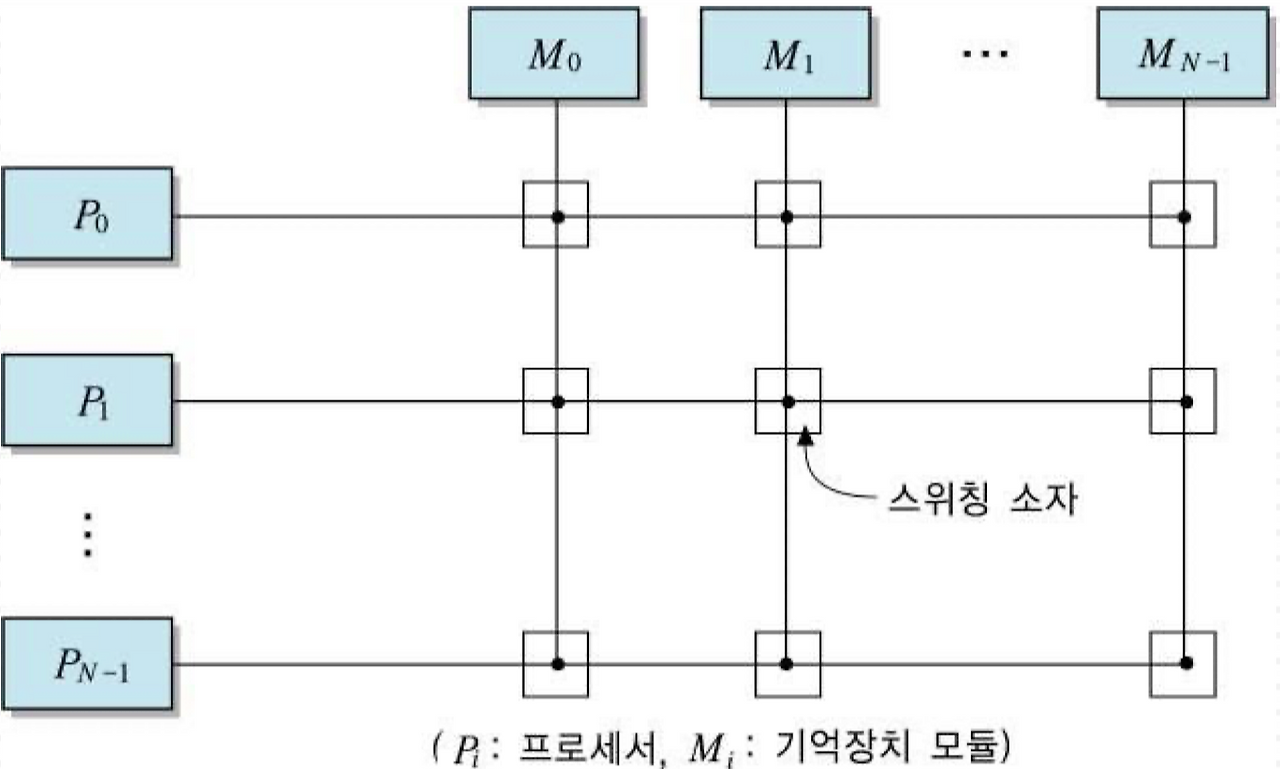
- 프로세서의 수가 많은 시스템에서는 버스 병목 현상을 줄이기 하여 높은 연결성을 제공하는 상호연결망 구조가 사용된다.
- ex) 크로스바 스위치의 구조는 다음과 같다.
다단계 상호연결망(MIN)
- 여러 단계들을 통하여 노드들을 연결해주는 네트워크
- 크로스바 스위치의 기본 개념을 이용하면서도 하드웨어 복잡성을 줄여주는 다단계 상호연결망도 여러가지 유형들이 제안되어 있다.
- ex) 오메가네트워크(omega network)를 분석

- 8개의 근원지 노드들과 8개의 목적지 노드들이 오메가 네트워크에 의해 연결되어 있는 구조를 보여주고 있다.
- MIN 구조에서 입력단과 출력단이 각각 N개인 경우에 필요한 단계의 수(s)와 각 단계의 스위칭 소자들의 수(m)를 구하는 일반식은 다음과 같다.


- 따라서 8 x 8 시스템은 세 개의 단계들로 구성되며, 각 단계는 네 개씩의 스위칭 소자들로 이루어진다.
- 각 스위칭 소자는 두 개의 입력단과 두 개의 출력단을 가지는 논리 회로로 구성된다.
각 입력과 출력을 연결해주는 연결 모드에는 다음과 같은 네 가지가 있다.
- 직진 : 같은 위치의 입출력 단자들이 서로 접속되는 모드
- 교차 : 서로 다른 위치의 입출력 단자들이 접속되는 모드
- 하위 방송 : 하단의 입력 단자가 모든 출력단자들로 접속되는 모드
- 상위 방송 : 상단의 입력 단자가 모든 출력단자들로 접속되는 모드
1번 노드와 7번 노드가 스위칭 소자들의 직진 혹은 교차 접속을 통하여 서로 연결된 예시이다.
이와 같은 연결리 서로 충돌하지 않는다면, 최대 8개의 근원지-목적지 노드들 간의 동시 연결도 가능해진다.
분산-기억장치 시스템 구조
선형 배열 구조
- 이 연결 구조는 N개의 노드들이 (N-1)개의 링크들에 의하여 차례대로 연결되며, 선형 배열(linear array)라고 부른다.
- 이 구조의 네트워크 지름은 (N-1)로서 다른 구조들에 비하여 평균 통신이 매우 길다.
- 네트워크 지름(network diameter)
- 네트워크 내에서 가장 멀리 떨어진 노드들 간의 거리
- 이 구조에서 가장 멀리 떨어진 노드들은 배열의 양 끝에 위치한 것들이며, 그들 간의 통신은(N-1)개의 링크들을 통해야 이루어질 수 있다.
- 선형 배열 구조는 연결 토폴로지가 간단하다.
장점
- 이 구조에서는 각 링크에서 동시에 전송 동작이 일어날 수 있으므로, 버스 구조보다 동시성이 더 높다.
단점
- 통신에 소요되는 시간이 노드들 간의 거리에 따라 서로 다르며, 노드의 수가 많아지면(N이 커지면) 통신 시간이 그에 비례하여 길어진다.

링 구조
- 선형 배열 구조에서 0번 노드와 (N-1)번 노드를 서로 연결해주는 링크를 하나 추가하면 링 구조가 된다.
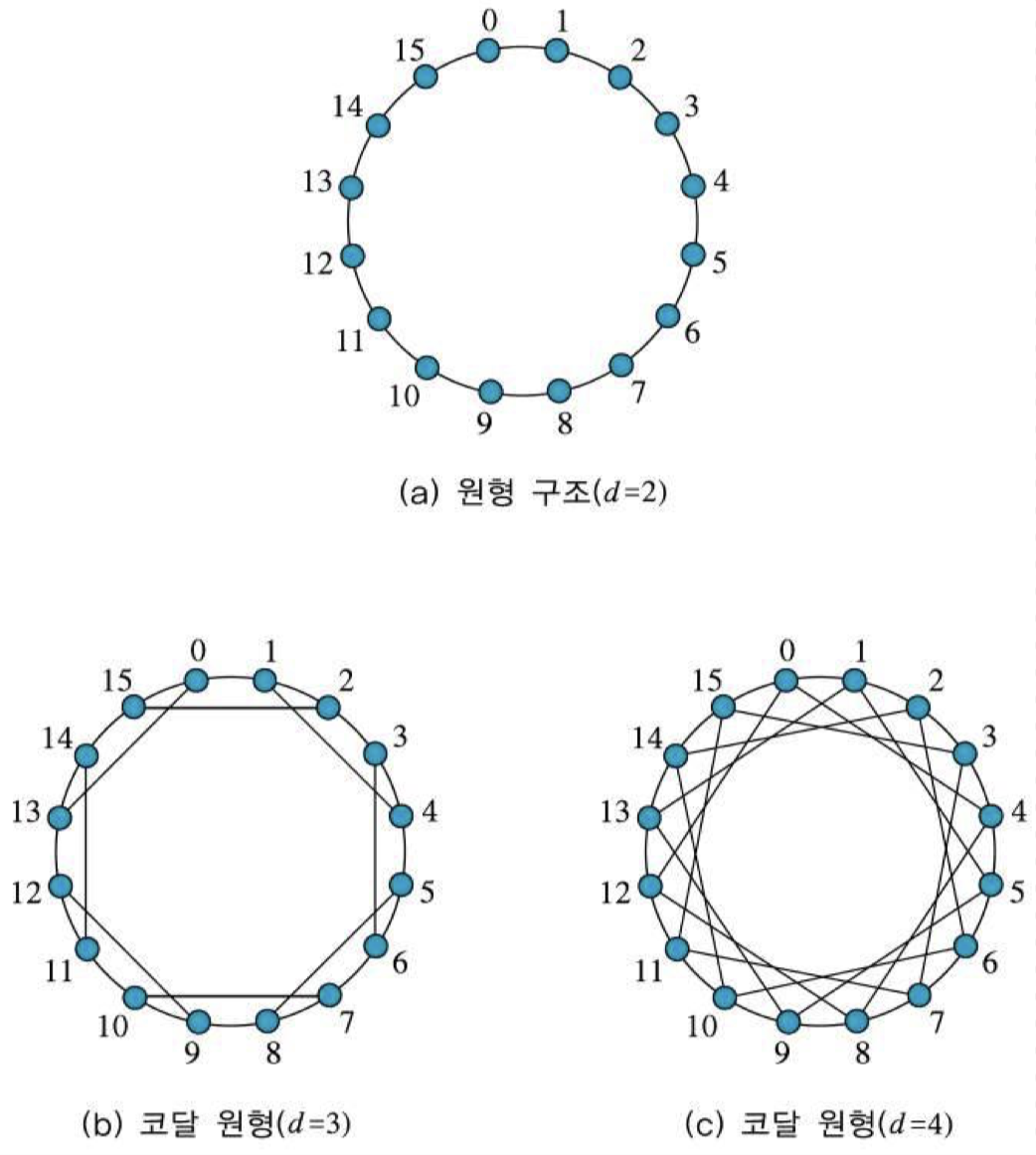
- 이 구조의 네트워크 지름은 각 링크가 양방향성이라면 [N/2]이 되고, 단방향성(uni-directional)이라면 (N-1)이 된다.
- 링 구조에서 링크의 수를 추가시킴으로써 각각 b, c와 같은 새로운 구조를 구성할 수 있다.
- 이러한 변형된 구조를 코달 링(chordal ring) 구조라고 부르며, 링크의 수가 증가될 수록 네트워크 지름은 감소된다.
- d는 각 노드가 가지는 링크의 수를 의미한다.
트리 구조

- 31개의 노드들이 다섯 층의 2진 트리(binary tree) 구조로 연결된 모습이다.
- 이러한 트리 구조가 완전히 안정된 모습을 가지기 위해서는 층(level)의 수를 k라고 할 때 N - (2^k-1)개의 노드들이 필요하다.
- 이 구조의 네트워크 지름은 2(k-1)이다. 이 구조는 시스템 요소들의 수가 증가함에 따라 성능이 선형적으로 향상되는 구조로 알려져 있으나, 네트워크 지름은 비교적 큰 편이다.
- 이와 같은 2진 트리는 팻 트리(fat tree) 구조로 변형될 수 있다.

- 이 변형된 구조는 상위 층으로 올라갈수록 노드간의 통신 채널 수가 증가흐는 특징을 가지고 있다. 따라서 이 구조는 트리 구조에서 상위 층으로 올라갈 수록 통신량이 많아져서 채널이 병목되는 문제점을 해결할 수 있으며, Thinking machine사가 개발한 슈퍼컴퓨터인 CM-5 시스템에서 실제로 사용되었다.
매시 구조
- 노드들을 2차원 배열로 연결하여 각 노드가 네 개의 주변 노드들과 직접 연결되는 구조를 매시 네트워크(mesh network) 라고 한다.
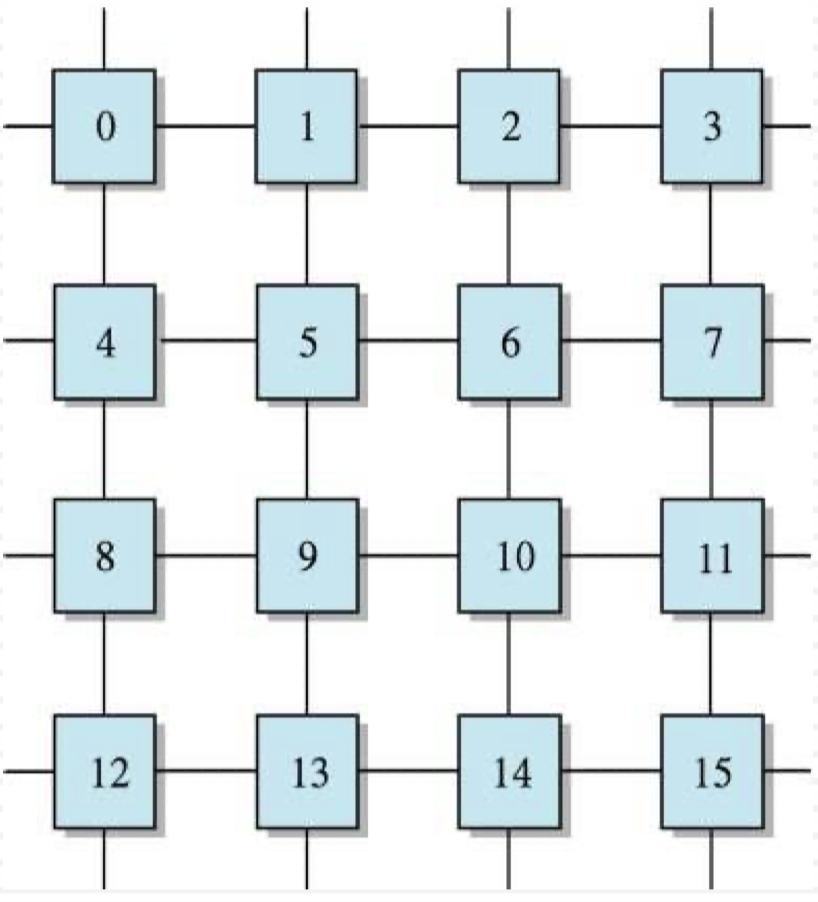
- 4x4 매시 네트워크의 기본 구조이며, 이 구조는 Illiac IV, MPP, DAP, CM-2 및 Intel Paragon같은 병렬컴퓨터들에서 실제로 사용되는데, 이 시스템들에서는 연결성을 높이기 위하여 기본 구조에 약간씩의 링크들을 추가하였다.
- 매시 네트워크의 변형된 구조로서 토러스 네트워크(torus network)가 있다.

- 토러스 구조는 매시 구조와 링 구조가 결합된 것이다. 즉, 행과 열의 노드들은 기본적으로 매시구조로 연결되며, 같은 행과 열의 노드들은 별도의 링으로 한 번 더 접속된다.
- 이 구조는 시스템 확장이 용이하다는 특징을 가지고 있다.
- 네트워크 지름은 k x k 토러스의 경우에 2[k/2]로서, 다른 구조에 비하여 짧은 편이다.
- 매시 및 토러스는 3차원 혹은 그 이상의 입체형 네트워크로 확장될 수도 있다.
- 그 경우에 전체 노드 수는 k의 n승으로 표현할 수 있는데, 여기서 k는 각 방향에 접속되는 노드의 수를 가리키며, n은 차원의 수이다.
- 그림의 구조는 k = 4, n = 2인 경우에 해당하므로, 전체 노드 수는 N = 4의 제곱 = 16이다.
- 그리고 만약 3차원 토러스로 구성한다면, N = 4의 3승 = 64개가 되며 3차원 토러스는 Cray T3E 슈퍼컴퓨터에서 사용되었다.
하이퍼큐브 구조
- 하이퍼 큐브(hypercube)는 k - 2인 n-차원 네트워크를 말한다.
- 이 네트워크는 2x2노드 구조들을 3차원 혹은 그 이상으로 접속하여 구성할 수 있다. 하이퍼 큐브에서는 노드들이 상호 연결 함수에 의해 서로 연결된다.

- 여기서, b는 노드 번호에 대한 2진수 표현의 각 비트를 나타낸다. 그리고 i는 시스템의 차원을 가리킨다. ex) n = 3인 3차원 하이퍼 큐브의 경우에는 전체 노드 수가 8개이므로, 노드 번호는 3비트로 구성된다. 따라서 위의 함수에서 i = 0, 1, 2에 대한 상호 연결 함수들을 각각 구하고, 그에 다라 노드들을 접속하여 구성하면 된다.
- 결과적으로 1차원 2차원 및 3차원 방향으로 서로 접속될 노드들의 번호를 가리키는 상호연결 함수들은 다음과 같아진다.

- C0 함수는 1차원(x) 방향으로 노드 번호의 최하위 비트(b0)의 값이 서로 보수인 노드들 간에 접속하면 된다는 것을 가리키고 있다. 그에 따라 x 방향으로 서로 접속되는 노드들의 번호를 나열하면, 000 <-> 001, 010 <-> 011 및 110 <-> 111이 된다.
- 그리고 2차원(y) 방향으로는 두 번째 비트(b1), 3차원 (z) 방향으로는 최상위 비트(b2)가 서로 다른 노드들 간을 접속하면 된다.
- 결과적으로 3차원 하이퍼 큐브는 다음과 같이 구성된다.

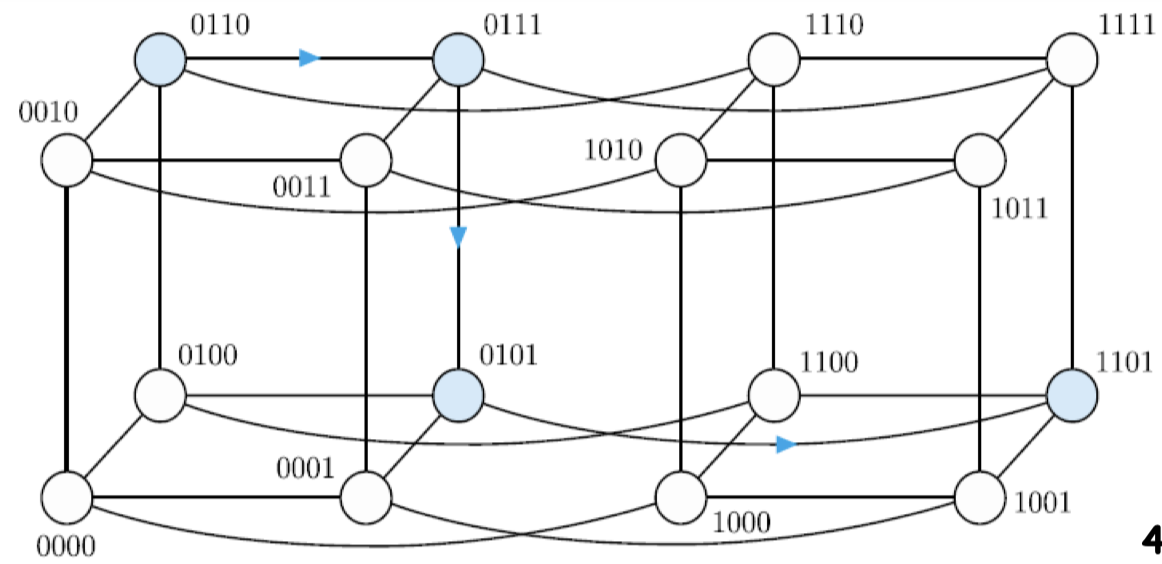
- 4차원 하이퍼큐브는 두 개의 3차원 구조를 이용하여 구성할 수 있다.
- 이 경우에는 전체 노드의 수가 2의 4승 = 16이므로, 노드 번호는 4비트로 이루어짐. 따라서 식의 함수로부터 C3(b3b2b1b0) = b3b3b2b1b0를 구할 수 있으며, 노드 번호의 최상위 비트인 b3의 값이 서로 다른 노드들을 서로 접속하면 된다는 것을 알 수 있다.
- 결과적으로, 그림에서와 같이 두 개의 3차원 구조에서 같은 위치에 있는 노드들을 네 번째 링크를 이용하여 서로 접속하면 4차원 하이퍼큐브가 구성된다.
- 이와 같이 구성된 하이퍼큐브에서는 노드들이 서로 간에 통신을 위하여 매시지-전송 방식을 이용한다. 즉, 전송할 노드가 데이터와 목적지 노드를 포함하는 패킷을 생성하여 수신할 노드로 보낸다.
패킷 전송을 위해서는 패킷이 두 노드 간의 경로를 스스로 찾아갈 수 있게 해주는 자동 경로설정 방법이 필요한데, 그 방법들 중의 한 예로서, E-큐브 라우팅이라고 불리는 경로설정 방식은 다음과 같다.
- 두 노드의 번호를 나타내는 2진수 비트들 간에 exclusive-OR 연산을 수행하여 방향 단어(direction word)를 구한다.
- 방향 단어의 LSB부터 검사하여, 비트 값이 1이면 x방향으로 이동하고 0이면 이동하지 않는다.
- MSB까지의 모든 비트들에 대하여 2번을 차례대로 반복하면서, 각 방향에 대하여 이동할 지를 결정한다.

- 하이퍼 큐브에서는 각 노드에 링크를 한 개씩만 추가하면, 전체 노드의 수를 두 배씩 증가시킬 수 있다. 즉, 구조 전체를 그 아래에 하나 더 위치시키고 같은 위치의 노드들을 서로 연결한다면, 노드의 수가 32개인 5차원 하이퍼큐브가 구성된다.
- 그보다 더 큰 시스템도 같은 방법을 이용하여 쉽게 구성할 수 있다.
- 즉, 차원을 하나씩 증가시킬 때마다 각 노드에 링크를 한 개씩만 추가하면 되며, 그 때마다 노드의 수는 두 배가 된다.
장점
- 하이퍼큐브 구조는 약간의 하드웨어 추가를 통하여 시스템을 쉽게 확장시킬 수 있다.
이 구조는 Intel iPSC 및 NCUBE/10과 같은 미니슈퍼급 컴퓨터시스템에서 사용됨.
Reference
컴퓨터 구조론 개정 5판
08장 고성능 컴퓨터시스템 구조
8.1 병렬처리의 개념 및 필요성 8.2 병렬처리의 단위 8.3 병렬컴퓨터의 분류 8.3.1 Flynn의 분류 8.3.2 기억장치 액세스 모델에 따른 분류 8.3.3 시스템 구성 방법에 따른 분류 8.4 다중 프로세서시스템 구
velog.io
'CS > 컴퓨터 구조론' 카테고리의 다른 글
| 컴퓨터 구조론 8장 [고성능 컴퓨터시스템 구조 / 그래픽처리유니트(GPU)] (0) | 2025.04.23 |
|---|---|
| 컴퓨터 구조론 8장 [고성능 컴퓨터시스템 구조 / 병렬컴퓨터의 분류] (0) | 2025.04.22 |
| 컴퓨터 구조론 8장 [고성능 컴퓨터시스템 구조 / 병렬처리의 개념 및 필요성, 병렬처리의 단위] (0) | 2025.04.22 |
| 컴퓨터 구조론 7장 [시스템 버스, I/O 및 인터럽트/DMA를 이용한 I/O] (0) | 2025.04.21 |
| 컴퓨터 구조론 7장 [시스템 버스, I/O 및 인터럽트 /인터럽트를 이용한 I/O] (0) | 2025.04.21 |